Perspicio, ergo expono
 
Lavoro di matematica svolto nell'ambito del progetto "Lauree scientifiche"
 
   
punto elenco Home
punto elenco Storia
punto elenco Teoria
punto elenco Mappa

 

  
 
   
punto elenco Il pH
punto elenco La magnitudo di un terremoto
punto elenco La magnitudo stellare
punto elenco Il numero e
punto elenco Il decadimento radioattivo
punto elenco La crescita delle cellule
punto elenco La crescita della popolazione
punto elenco La crescita bancaria
punto elenco La spirale logaritmica
punto elenco La legge di Weber e Fechner
punto elenco La legge di Titius-Bode
punto elenco La scala musicale temperata
punto elenco Il decibel

 

  
   
punto elenco Progetto
punto elenco Traccia
punto elenco Schede
punto elenco Relazione

 

  
Le funzioni esponenziali
 

 

Prefissato un numero reale a > 0, è possibile associare ad un qualsiasi numero reale x, il numero reale ax. In tal modo è possibile considerare x come una variabile reale e definire una funzione f avente come dominio R tale che

                                            f : x ------->   ax

Resta cosi definita una funzione reale di variabile reale, di equazione y = ax, che si chiama funzione esponenziale di base a, il cui dominio è R.

Il caso banale in cui è a = 1  non è preso in considerazione poiché, essendo 1x = 1 per qualunque x appartenente ai numeri reali, la funzione non è altro che quella costante di equazione y =1.

Cerchiamo ora di rappresentare graficamente  una funzione esponenziale con base a > 1. A tal fine scegliamo a = 2 e otteniamo un certo numero di coppie (x;y) appartenenti al grafico di y = 2x. La tabella seguente indica alcuni dati utili per poter rappresentare graficamente la funzione.

                       

 

Ora andiamo a rappresentare il grafico della funzione esponenziale y = 2x.                         

 

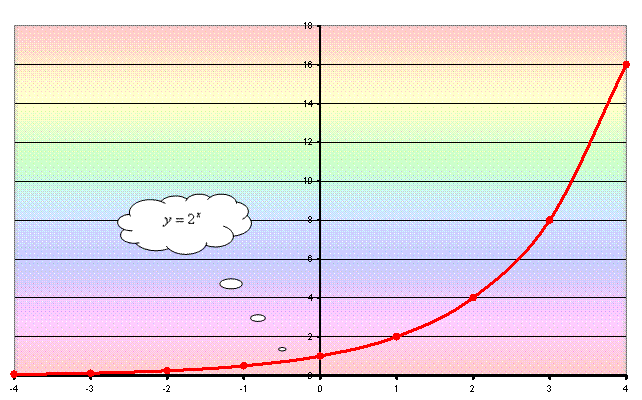
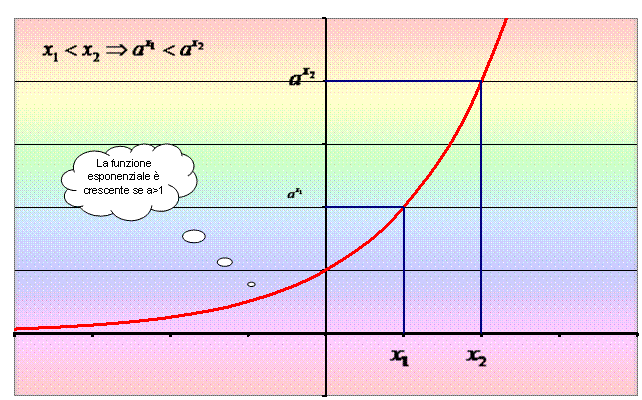
Osserviamo che la funzione è crescente. Intuitivamente, una funzione è crescente quando "spostandoci verso destra sull'asse delle ascisse, ci si sposta verso l’alto sull'asse delle ordinate". Per formalizzare meglio la definizione, diciamo che la funzione y = ax  è crescente in un intervallo (a,b) se per ogni coppia x1, x2 in (a, b), con x1 < x2, si ha ax1 < ax2.

 

Rappresentiamo ora graficamente  una funzione esponenziale con base a tale che 0 < a < 1. A tal fine scegliamo la base a = ½  e otteniamo un certo numero di coppie (x,y) appartenenti al grafico di y = (½)x. La tabella seguente indica alcuni dati utili per poter rappresentare graficamente la funzione.

 Ora andiamo a rappresentare il grafico della funzione esponenziale y = (1/2)x .

 

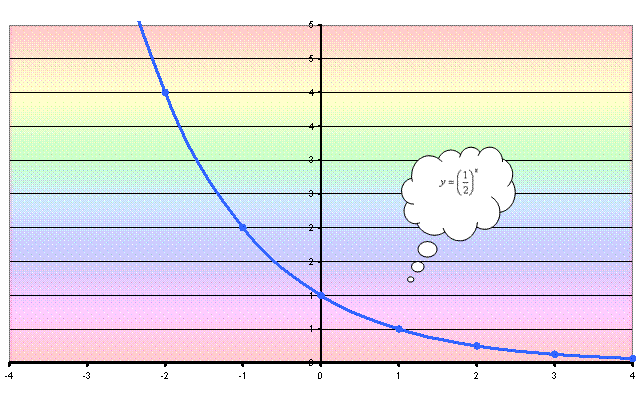
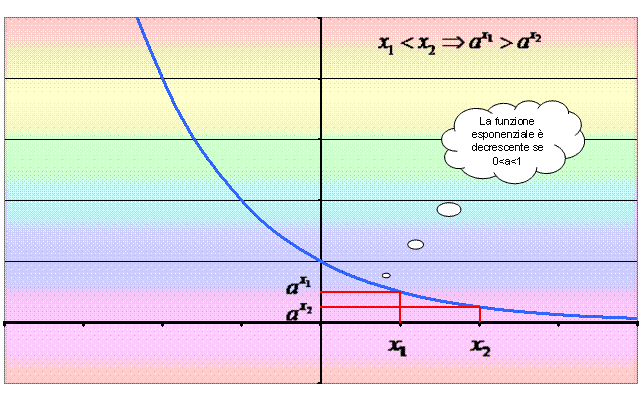
Intuitivamente una funzione è decrescente quando "spostandoci verso destra sull'asse delle ascisse, ci si sposta verso il basso sull'asse delle ordinate". Per formalizzare meglio la definizione, diciamo che la funzione y = (1/2)x è decrescente nell’intervallo (a, b) se per ogni coppia x1, x2 in (a, b), con x1 < x2, si ha (1/2)x1 > (1/2)x2.

 

Tutte le funzioni esponenziali:

  • si trovano solo nel primo e secondo quadrante, ossia la y assume valori solo positivi;

  • intersecano l'asse delle ordinate nel punto (0, 1);

  • non intersecano l’asse delle ascisse, ma hanno un asintoto orizzontale di equazione y = 0.

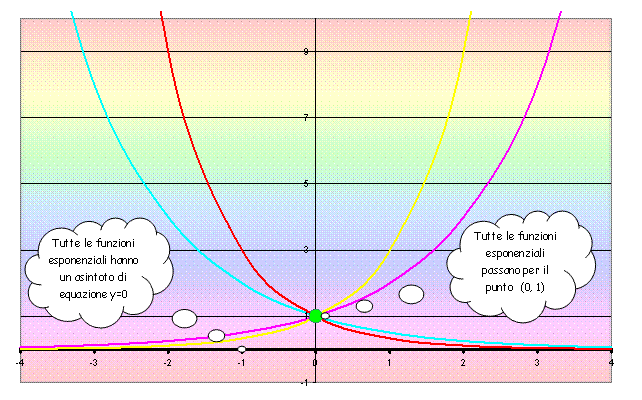
Inoltre, possiamo anche dire che, per ogni base a,  i  grafici delle funzioni esponenziali di equazioni y = ax e y = (1/a)x sono l'uno il simmetrico dell'altro rispetto all’asse delle ordinate.

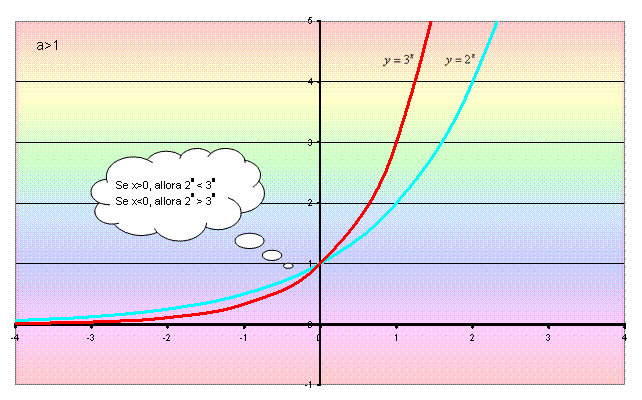
Infine, per quanto riguarda le funzioni esponenziali con a >1, possiamo osservare, per esempio, che:

  • se x>0, allora 2x < 3x;

  • se x<0, allora 2x > 3x.

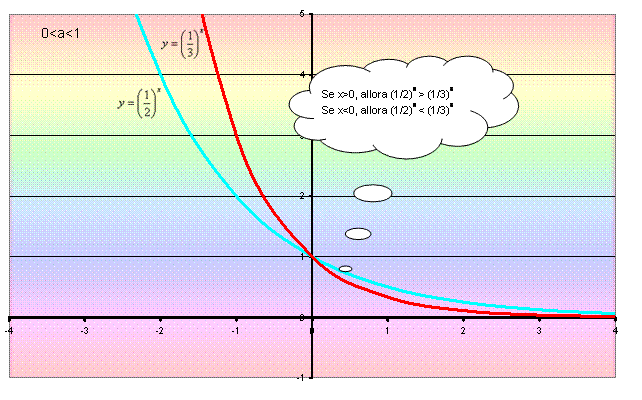
Invece, per quanto riguarda le funzioni esponenziali con 0 < a < 1, possiamo osservare, per esempio, che:

  • se x>0, allora (1/2)x > (1/3)x;

  • se x<0, allora (1/2)x < (1/3)x.

 

  

Le funzioni logaritmiche
   

Le funzioni esponenziali risultano biunivoche, se a è diverso da 1, e quindi sono dotate di inversa. Ciò equivale a dire che, fissato un numero reale y>0, esiste un unico x che risolve l’equazione  ax = y. Il dominio della funzione inversa sarà, pertanto, l'insieme dei numeri reali positivi, mentre il codominio sarà R.

La funzione inversa della funzione  esponenziale è detta funzione logaritmo in base a, dove a>0, ma  diverso da 1. Essa, formalmente , si scrive in questo modo:

x = loga y.

Non è difficile capire, dunque, che il logaritmo di un numero è l'esponente da dare alla base a per ottenere y.

Cerchiamo ora di rappresentare graficamente  una funzione logaritmica con base a > 1. A tal fine scegliamo a = 2 e otteniamo un certo numero di coppie (x;y) appartenenti al grafico di y = log2 x. La tabella seguente indica alcuni dati utili per poter rappresentare graficamente la funzione.  

Ora andiamo a rappresentare il grafico della funzione esponenziale y = log2 x.  

 

Osserviamo che:

  • la funzione e' sempre crescente;
  • e' definita solo per valori positivi della x;
  • ha un asintoto verticale nell'asse y, di equazione x = 0 ;
  • il punto (1,0) e' sempre di intersezione fra la curva e l'asse delle x;

Cerchiamo ora di rappresentare graficamente  una funzione logaritmica con base 0 <a < 1. A tal fine scegliamo a = 1/2 e otteniamo un certo numero di coppie (x;y) appartenenti al grafico di y = log1/2 x. La tabella seguente indica alcuni dati utili per poter rappresentare graficamente la funzione.  

Ora andiamo a rappresentare il grafico della funzione esponenziale y = log1/2 x.  

Possiamo osservare che:

  • la funzione e' sempre decrescente;
  • e' definita solo per valori positivi della x;
  • ha un asintoto verticale nell'asse y di equazione x = 0;
  • il punto (1,0) e' sempre di intersezione fra la curva e l'asse delle x; 

Possiamo anche osservare che i grafici delle funzioni logaritmiche di equazioni 
 y = loga x e y = log1/a x 
sono  l'uno il simmetrico dell'altro rispetto all’asse delle ascisse.

Per quanto riguarda le funzioni logaritmiche con a >1, possiamo osservare, per esempio, che:

  • se 0<x<1, allora log2 x < log3 x ;

  • se x>1, allora log2 x > log3 x .

Invece, per quanto riguarda le funzioni logaritmiche con 0 < a < 1, possiamo osservare, per esempio, che:

  • se 0<x<1, allora log1/2 x > log1/3 x ;

  • se x<1, allora log1/2 x < log1/3 x .

Infine, confrontiamo i grafici  delle  funzioni y = ax  e y = loga x nel caso a>1:

e in quello per cui 0<a<1: