|
Il numero
e non è
molto noto al di fuori dell’ambiente matematico. Eppure è un numero che
gioca un ruolo fondamentale non solo in matematica, ma in tante
applicazioni, come abbiamo occasione di vedere in questo sito.
Il numero e è
irrazionale ossia fa parte di quei numeri le cui cifre
decimali
si seguono quasi casualmente, senza nessuna regola, se non quella che
definisce il numero stesso. Al contrario, i numeri razionali, dopo un
certo numero di cifre decimali, hanno tutti zeri o sequenze di cifre che
si ripetono periodicamente: essi possono essere messi sotto forma di
frazione con numeratore e denominatore interi, da cui il nome dal latino
“ratio” nel significato di rapporto.
Ma “ratio” significa
anche ragione, come dire che razionali sono quei numeri sui quali si può
ragionare, mentre gli irrazionali sono numeri non ragionevoli,
stravaganti, quasi folli.
A dire il
vero, il
numero e per un istante dà la speranza della razionalità in quanto,
dopo la prima cifra decimale, si ripete la sequenza 1828. Tuttavia, la
speranza è presto frustrata poiché, dopo la prima ripetizione, le cifre
riprendono a seguirsi in modo apparentemente casuale :
2,7182818284590...
Il
numero e viene detto anche trascendente perché non c’è un’equazione
polinomiale a
coefficienti razionali che lo ammetta come soluzione: si sfiora la
teologia.

Anche se
a Nepero può essere attribuita la scoperta del numero e, esso fu
utilizzato da costui solamente per introdurre i logaritmi nel suo libro
Mirifici logarithmorum canonis descriptio; ad Eulero,
invece, va il merito di averlo approfondito, di averlo reso
popolare e indicato col nome che ben conosciamo.
Il numero e
può essere introdotto come limite della successione
sn=(1+1/n)n:
la tabella sottostante indica
alcuni termini di tale successione.

Osserviamo che la
successione sn
è
crescente, dato che ogni termine é maggiore del precedente, limitata
superiormente poiché ogni termine é minore di tre e, quindi,
convergente ossia esiste un numero al quale la successione tende ad
avvicinarsi sempre più; ossia, un numero la cui differenza
con un elemento della successione può essere resa minore di qualsiasi
quantità, scegliendo opportunamente n.
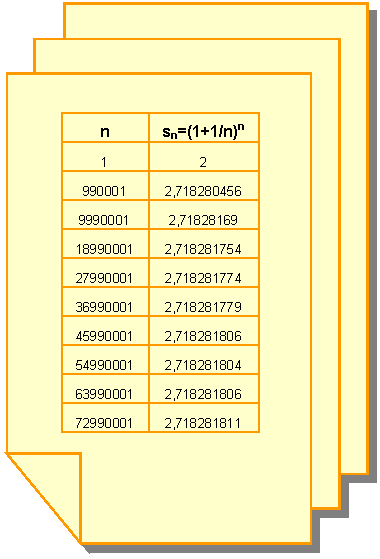
Analizzando, attraverso l'aiuto del foglio elettronico EXCEL, i valori
assunti dai termini della successione, si nota che per valori di n molto
grandi (potremmo dire per n tendente a infinito) il valore di sn
tende al numero e.

Il numero
di Nepero frequentemente è utilizzato come base per i logaritmi: in
questo caso, i logaritmi nella base a = e sono scritti nella forma logex
= lnx e sono chiamati logaritmi naturali o neperiani. Questa base
permette di avere notevoli semplificazioni in numerose formule
fondamentali.
Generalmente, però,
un numero reale viene espresso nella rappresentazione in base 10 e solo
in contesti particolari (per esempio, nell’ambito informatico) lo si
esprime in una diversa base (2 o 16). È, quindi, naturale scegliere come
base dei logaritmi il numero 10 cioè a=10. In tal caso i logaritmi si
dicono decimali. Conviene, inoltre, scegliere una notazione che ci
risparmi di riportare continuamente la base 10. Scegliamo, pertanto, di
scrivere:
log10x=
logx
Poiché la base "e" e
la base "10" sono quelle più usate, può essere interessante determinare
il coefficiente che collega questi due sistemi di logaritmi, così da
poter passare facilmente da un sistema all'altro.
Considerando la nota
formula che consente il passaggio da una base ad un'altra:
logax = (logbx)/(logba)
e ponendo: a =e e
b=10, si ottiene:
lnx = logx/loge
Poiché loge~0,43429448
e, pertanto, 1/loge~2,302585094, si ha:
lnx~2,302585094*logx
che rappresenta il
legame tra i logaritmi nelle due basi prese in considerazione.
Di seguito sono
riportati i grafici delle funzioni y=logx e y=lnx
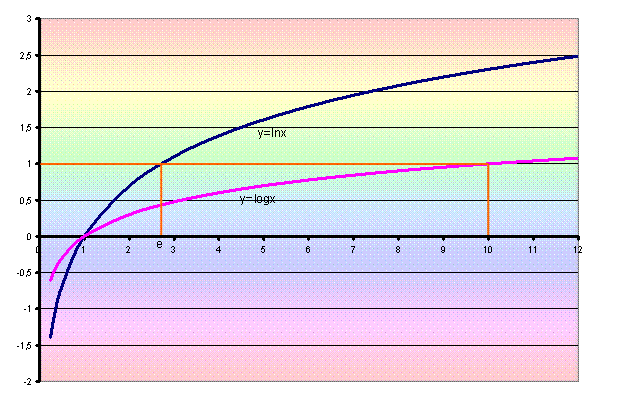
In relazione a
quanto detto precedentemente, il grafico di y=lnx si ottiene da
quello di y=logx, moltiplicando quest’ultima funzione per il fattore
2,302585….
Si può osservare,
infine, che spesso risulta utile esprimere una funzione esponenziale di
base a qualsiasi come una funzione in base e. A tal fine si ottiene che:
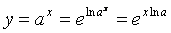
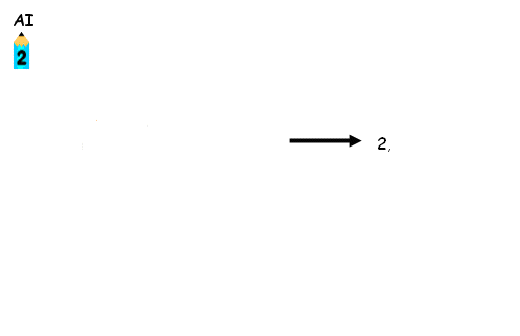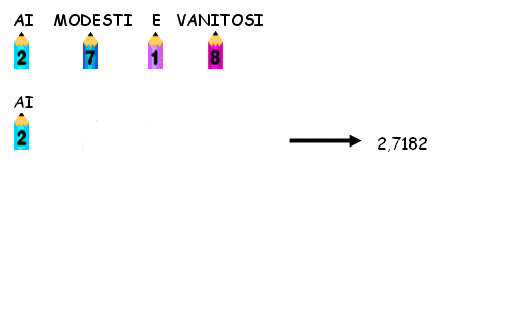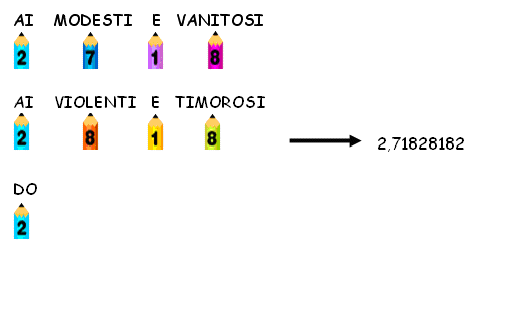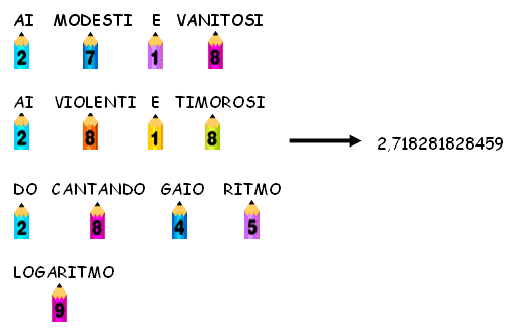
Per
concludere, presentiamo una poesia che Giorgio Rabbeno, un poeta
della matematica, ha
scritto nel 1935 per ricordare le prime cifre del numero e al fine
di
partecipare ad un
corcorso ideato dalla rivista Sapere:
Ai
modesti o vanitosi
ai
violenti o timorosi
do,
cantando gaio ritmo,
logaritmo...
 |
