| |
Una spirale è una curva che si
avvolge attorno a un determinato punto centrale o asse, avvicinandosi o
allontanandosi progressivamente, a seconda di come un punto si muove;
pertanto, non ha un punto di inizio, ma prosegue infinitamente sia verso
l’interno che verso l’esterno, mantenendo la sua forma al variare della
scala di osservazione.
In
particolare, la spirale logaritmica, o equiangolare, fu studiata
da Renato Cartesio nel 1638 e può essere distinta da un'altra ben nota
spirale, quella di Archimede, per il fatto che le distanze fra i bracci
di una spirale logaritmica aumentano secondo una progressione
geometrica, mentre in quella archimedea le distanze sono uguali.
Verso la
fine del 1600, il matematico Jackob
Bernoulli scoprí molte proprietà della spirale logaritmica e ne
rimase talmente affascinato che chiese di averne una scolpita sulla sua
pietra tombale, accompagnata dalla scritta latina "Eadem mutata resurgo"
(Sebbene cambiata, rinasco identica). Purtroppo la spirale che ancora
oggi è visibile sulla lapide del matematico a Basilea è una spirale di
Archimede; la scritta invece non compare.
Una spirale
logaritmica si può ottenere considerando una semiretta che ruota
uniformemente intorno ad un suo estremo e un punto che si muove lungo
questa semiretta con una velocità che aumenta man mano che il punto si
allontana dall’estremo fissato. La curva tracciata dal punto in
movimento è, appunto, una spirale logaritmica.
L'equazione della curva, in coordinate polari (r, θ), può essere scritta
come
r = ρkθ
in cui
k è una costante reale e ρ una costante reale e positiva.
Poiché θ
può essere ricavato dalla relazione precedente tramite l'applicazione
dei logaritmi,
è nato il termine "spirale logaritmica".
I grafici
sottostanti danno una rappresentazione della curva, ottenuta, tramite il
foglio elettronico EXCEL, ponendo ρ=0,8 e variando k.
 |
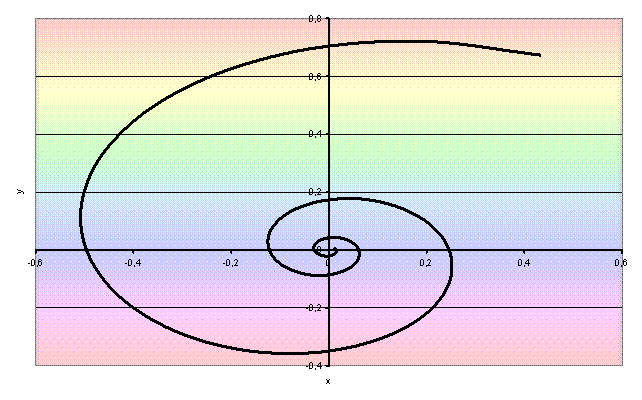
Se k>0
la spirale si avvolge intorno al punto centrale in senso
antiorario: |
 |
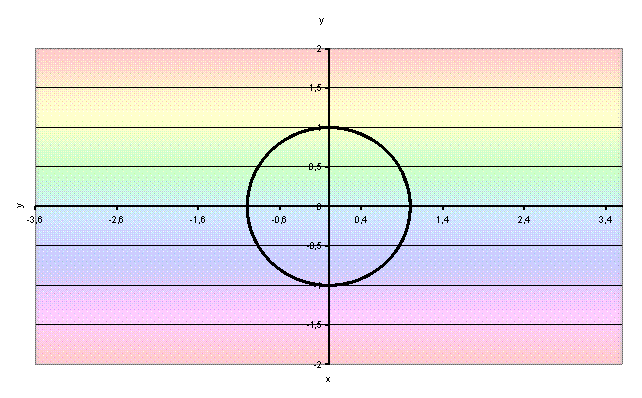
Se k=0
la spirale degenera in una circonferenza: |
 |
Se k<0
la spirale si avvolge intorno al punto centrale in senso orario: |
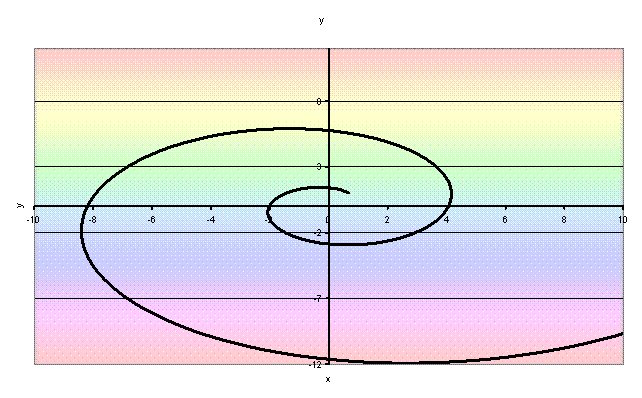
La spirale
logaritmica può essere realizzata utilizzando i numeri di Fibonacci;
pertanto, prima di provare a disegnare la curva in tal modo, cerchiamo di spiegare di
che cosa si tratta.
Nel 1223, l’imperatore Federico II di Svevia indisse una gara sui calcoli
matematici; il vincitore di tale competizione fu Leonardo "da Pisa", conosciuto
anche con il nome di Fibonacci.
Nella
seguente tabella sono riportati i primi dieci numeri della serie
che lo fece vincere:

Ogni
numero della sequenza è la somma dei due numeri precedenti.
Esempio:
3+5=8; 13+21=34; 55+89=144; ecc...
La
sequenza
presenta alcune proprietà:
 |
Se si
sommano due o più numeri consecutivi di tale serie, sempre partendo dal
primo, e si aggiunge ulteriormente 1, si ottiene sempre un altro numero
che nella sequenza segue di due posti l’ultimo termine della somma. |
Esempio:
1+1+2+3+5+1=13
In questo
caso si sono sommati i primi cinque numeri di Fibonacci, si è aggiunto 1
e si è ottenuto il settimo numero della sequenza.
 |
Il
rapporto tra un termine e quello successivo si avvicina
molto rapidamente a 0,618..., mentre il rapporto tra un termine
e quello precedente si avvicina altrettanto rapidamente a
1,618...; |
Esempi:
1:2=0,500
8:13=0,615
2:3=0,667 13:21=0,619
3:5=0,600 21:34=0,618
5:8=0,625 34:55=0,618
Il numero
0,618..., indicato dalla lettera greca
Φ, è detto rapporto
aureo: è un numero irrazionale con molte curiose e misteriose
proprietà...;
 |
Il
rapporto tra un numero della sequenza e quello che lo precede di
due posti è sempre
pari (tendente a) 2,618..., che è il quadrato di 1,618...;
|
 |
Se
si prendono due numeri consecutivi della serie, la somma dei loro
quadrati è un altro numero che nella sequenza occupa il posto
risultante dalla somma delle posizioni dei due termini di partenza.
|
Esempio:
32+52=34
In questo
caso si sono presi il quarto e quinto numero della serie, se ne è fatto
il quadrato e la somma dei quadrati è risultata essere il nono numero
della sequenza.
 |
Il
quadrato di qualsiasi numero della serie è uguale al numero che
lo precede per il numero che lo segue, più o meno 1. Il più o
meno si alterna lungo la sequenza; |
 |
Se
dividiamo qualsiasi numero della sequenza per quello che lo precede
di due posti, otterremo sempre due come quoziente, e come resto il
numero immediatamente precedente il divisore;
|
Esempio:
89:34 = 2 con il resto di 21.
 |
Il
quadrato di un numero di Fibonacci meno il quadrato del
numero che lo precede di due posti è sempre un numero della successione;
|
 |
Il
massimo comun divisore di due numeri di Fibonacci è ancora un
numero di Fibonacci; |
 |
Consideriamo la sequenza ottenuta moltiplicando per 4 tutti i
numeri della serie di Fibonacci, esclusi 1 e 2:
|
12 20 32 52
84 ...
Ad ogni numero di tale sequenza
aggiungiamo, nell'ordine, i numeri della serie di Fibonacci. Otteniamo:
13 21 34 55
89 ...
che è ancora la serie di
Fibonacci privata di alcuni termini iniziali.
Il numero
0,618... è importante perchè è il rapporto della sezione aurea.
Vediamo di che cosa si tratta.
Dividiamo un segmento di
lunghezza 1 in due parti, una di lunghezza x e l'altra
di lunghezza 1-x, tali che
(1-x) : x = x : 1
Per risolvere la proporzione si
ricorda che il prodotto degli estremi è uguale al prodotto dei medi, per
cui si ottiene:
x² = 1- x
cioè
x² + x - 1 = 0
Possiamo ricavare
dall'equazione di secondo grado ottenuta le soluzioni:
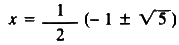
Scopriamo
così che la soluzione positiva è
x = 0,618...
Consideriamo ora un
rettangolo ABCD con i lati in rapporto aureo AD/AB = 1,618... Se al suo
interno tracciamo il quadrato di lato CD, il rettangolo restante avrà i lati
in rapporto aureo AB/AE = 1,618...
Se ripetiamo questa operazione infinite volte, otterremo sempre dei rettangoli con i lati
in rapporto aureo tra loro.
Dopo le precedenti
osservazioni, mostriamo che si può disegnare
una spirale logaritmica, utilizzando i numeri di Fibonacci.
|
Consideriamo un
quadrato ABCD di lato AB=1.
Costruiamo sul lato AB=1
il quadrato ABEF e, centrando in A, tracciamo l’arco di
circonferenza BF. |
 |
|
Sul lato FE=DA+AF=1+1=2
costruiamo il quadrato FGHD e, centrando in D, tracciamo l’arco
di circonferenza EH. |
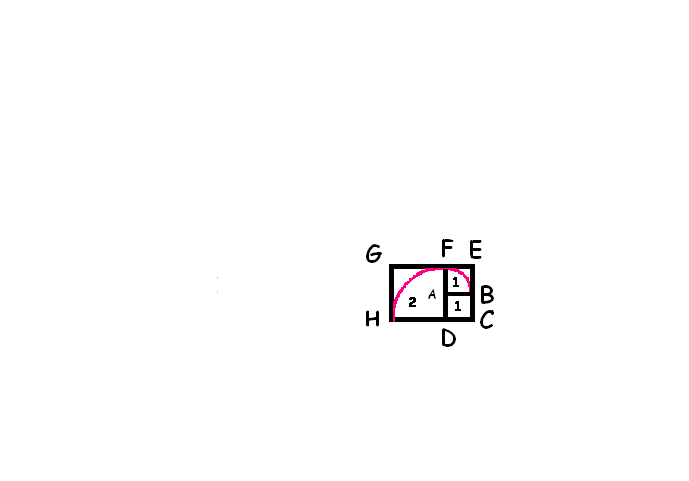 |
|
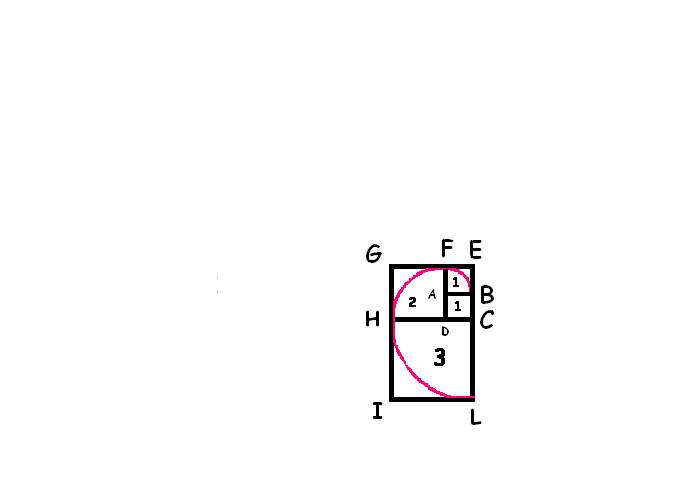
Sul lato CH=CD+DH=1+2=3
costruiamo il quadrato CHIL e, centrando in C, tracciamo l’arco
di circonferenza HL. |
 |
|
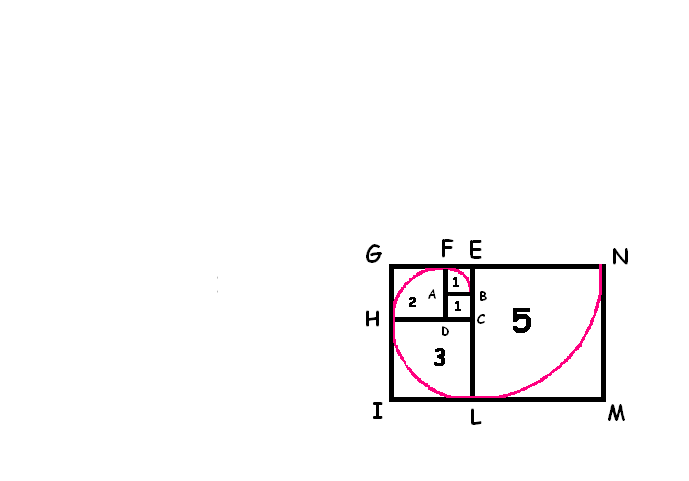
Sul lato EL=EC+CL=2+3=5
costruiamo il quadrato ELMN, centrando in E, tracciamo l’arco di
circonferenza LN. |
 |
|
Sul lato GN=GE+EN=3+5=8
costruiamo il quadrato GNOP e, centrando in G, tracciamo l’arco
di circonferenza PN. |
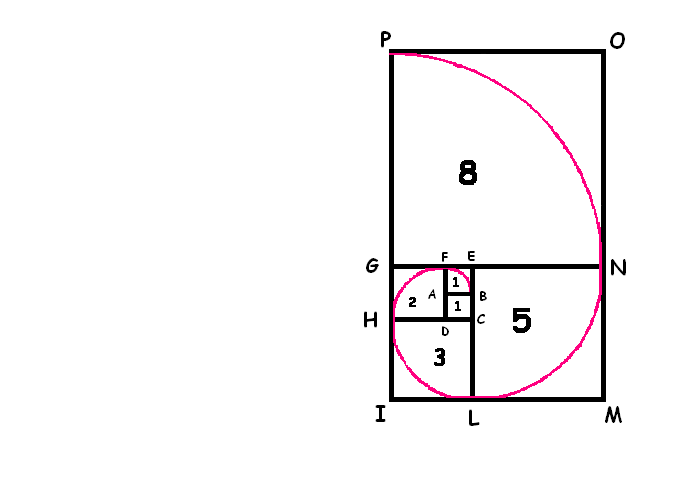 |
|
Sul lato
PI=PG+GI=5+8=13 costruiamo il quadrato PQRI e, centrando in H,
tracciamo l’arco di circonferenza RP. |
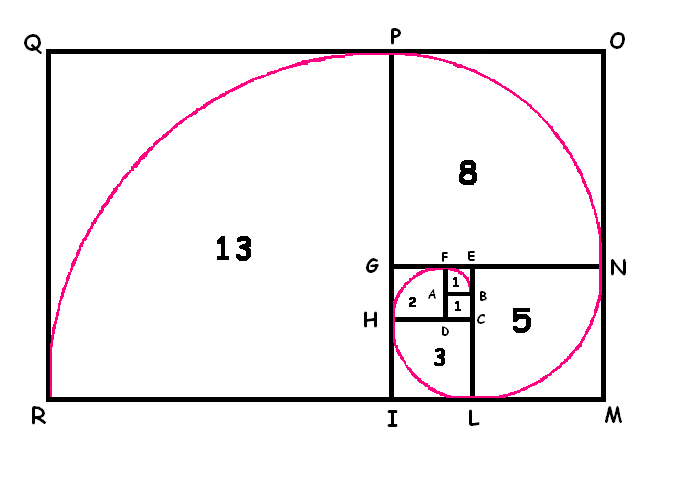 |
| Il procedimento
precedente può essere iterato e la spirale prosegue
all'infinito. |
 |
|
 |
|
|
