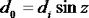Distanza di due punti lontani tra loro e situati su differenti livelli

Vogliamo misurare la distanza di due punti lontani tra loro e situati a differenti livelli. Consideriamo come superficie di riferimento un piano orizzontale con quota pari a quella media della zona in esame.

La distanza che viene misurata è la distanza inclinata di, cioè la congiungente il centro dello strumento per fare la misura con il punto da misurare.  Considerando l'angolo zenitale z, ben visibile nella figura sottostante,

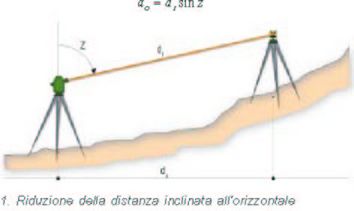
e la distanza orizzontale d₀,  si trova facilmente, applicando un noto teorema di trigonometria relativo ai triangoli rettangoli, che:

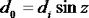
Lunghezza di un segmento verticale i cui estremi sono inaccessibili

Vogliamo determinare l’ altezza AB =x di una torre o di una montagna la cui base A non sia accessibile.

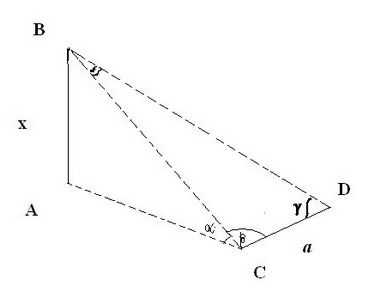
Misuriamo sul terreno una base CD lunga a che non sia orizzontale e non sia posta in uno stesso piano verticale con AB, ma tale però che il punto C sia sul piano orizzontale passante per A.

Misuriamo  i tre angoli:

AĈB = α

BĈD = β

CDB = γ

L’angolo α, se il punto A non è visibile, è l’angolo che la visuale BC forma con l’orizzontale.

Dal triangolo BCD, con il teorema dei seni, si trova la misura BC:

BC : sen γ =  a : sen [180º-( β+ γ)]

  BC= a sen γ / sen ( β+ γ)

Quindi, dal triangolo rettangolo BAC, si ha:

          AB = x = BC sen α = a sen α sen γ / sen (β+ γ)

Distanza tra due punti separati da un ostacolo

Vogliamo determinare la distanza x tra due punti A e B separati da un ostacolo, ma ambedue accessibili.

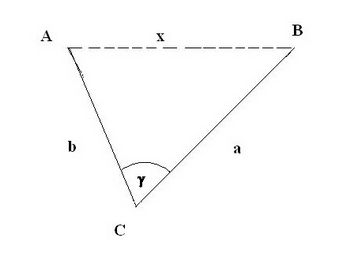
Fissiamo un punto C, distante dai punti A e B rispettivamente b ed a e dal quale i due punti siano visibili; misuriamo l’angolo ABC = γ

Del triangolo ABC sono noti due lati e l’angolo compreso, perciò la distanza AB è calcolabile con il teorema del coseno o di Carnot.

Se i due punti A e B sono visibili l’uno dall’altro, ma solo B è accessibile, come nel caso della figura sottostante,

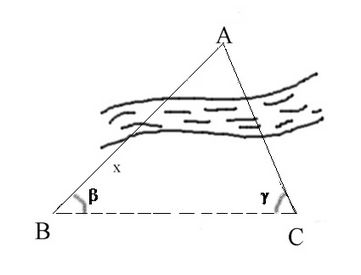
si misura una base BC= a tale che da C sia visibile il punto A, poi si misurano gli angoli β e AĈB= γ e dal triangolo ABC, col teorema dei seni, si ottiene:

x: sen γ = a : sen [180º-( β+ γ)] 

x= a sen γ / sen ( β+ γ)

Distanza fra due punti entrambi inaccessibili

Vogliamo trovare la distanza tra due punti A, B inaccessibili, ma visibili.

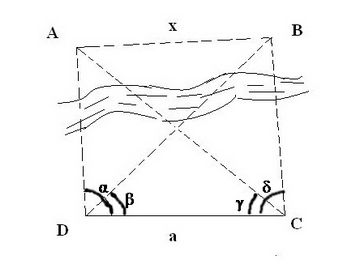
Scelta una base CD = a,

si misurano gli angoli ADC= α ; BDC= β ; DĈA = γ ; BĈD = δ.

Dai triangoli ACD e BCD, per il teorema dei seni, si ha:

AC : sen α = a : sen (α + γ)

BC : sen β = a : sen  (β + δ)

cioè

AC = a sen α / sen (α + γ)

BC = a sen β / sen  (β + δ)

Ora del triangolo ACB si conoscono i lati AC, BC e l’angolo compreso δ-β, quindi col teorema del coseno o di Carnot potremo trovare la distanza incognita AB.

Calcolo della distanza della terra dalla luna

Vogliamo trovare la distanza di un punto A della Terra (punto accessibile) da un punto L inaccessibile, ma visibile, quale può considerarsi la Luna.  A tal fine,  usiamo il metodo seguito nella distanza tra due punti separati da un ostacolo; però, trattandosi di una distanza piuttosto grande (qualche centinaia di migliaia di chilometri), conviene prendere sulla Terra la base AB di parecchi chilometri, per avere angoli di visuale non troppo piccoli. Prendiamo come base la corda AB che sottenda un arco di meridiano terrestre nel cui piano (piano meridiano) vi sia anche il punto L che rappresenta la Luna, come possiamo osservare nella figura sottostante.

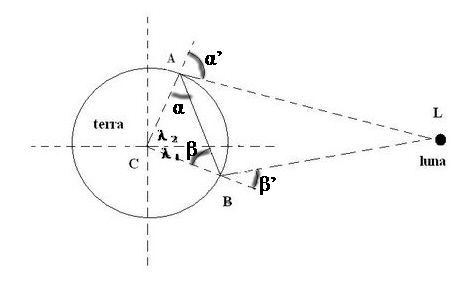
Per trovare la lunghezza  di AB si considera  il triangolo  ABC, dove C è il centro della terra.

Con osservazioni astronomiche si misurano le latitudini di A (λ₁ ) e di B (λ₂) e se A, B sono da bande opposte dell’equatore si ha AĈB = λ₁+ λ₂.

Si trovano poi le lunghezze dei raggi CA e CB dato che si conoscono le latitudini di A e B; a questo punto, del triangolo ABC si conoscono quindi due lati e l'angolo compreso, per cui si trovano: la misura c di AB  e le misure di CAB = α e di CBA = β; poi si misurano direttamente gli angoli α' e  β'  che le verticali CA e CB formano rispettivamente con le visuali AL e BL.

Infine si ha LÂB= 180°-(α + α') e  ABL=180°-(β + β' ) ; così del triangolo ABL si conoscono un lato e i due angoli adiacenti e risolvendo il triangolo si ottiene la distanza AL di circa km 384100 cioè circa 60,27 volte il raggio equatoriale terrestre.

Calcolo della distanza della terra dal sole

Per trovare la distanza della terra dal Sole, si può usare anche il metodo precedente, ma, poichè la distanza Terra-Sole è enorme, non è possibile trovare sulla Terra una base adeguata, per cui si ricorre alla parallasse del Sole.

La parallasse di un astro S, rispetto ad un punto P sulla Terra, è l'angolo sotto cui è visto il raggio terrestre dal centro S dell'astro, cioè l'angolo OSP nella figura sottostante.

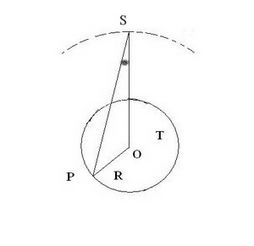
La parallasse varia col moto della Terra e dell'astro.

Se il raggio terrestre OP è perpendicolare alla congiungente SP, la parallasse si dice equatoriale orizzontale, come si vede nella figura seguente:

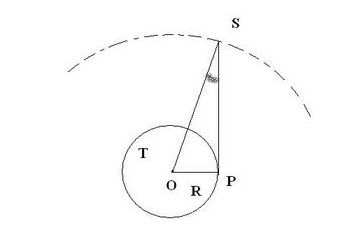
Per calcoli di astronomia, si sa che la parallasse equatoriale orizzontale del Sole è di circa 8'',8; quindi, la distanza Terra-Sole SO si ottiene considerando il triangolo rettangolo OPS e, precisamente, facendo il seguente calcolo:

OS = OP / sin8'',8

e poichè

OP = R = km 6367,397

si trova

OS = km 150000000 circa.

Calcolo della lunghezza del raggio della terra (supposta sferica)

Consideriamo la seguente figura in cui sia AB un arco di meridiano e φ l'ampiezza del corrispondente angolo al centro.

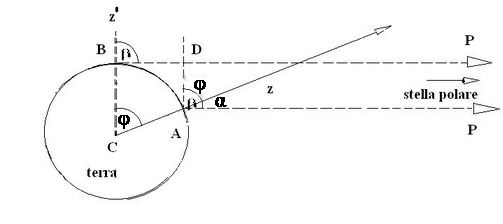
La lunghezza l dell'arco AB può essere calcolata mediante un procedimento detto della "triangolazione geodetica", misurando, mediante la risoluzione di triangoli, le lunghezze degli archi AP, PQ, ..., SB.

L'angolo φ è dato dalla differenza fra gli angoli α e β che sono detti distanze zenitali della stella polare P, in B e in A.

Bisogna osservare che, data l'enorme distanza della Terra dalla stella polare, le visuali AP e BP si possono ritenere parallele.

Note le misure di l e di φ, si trova facilmente la misura R del raggio terrestre, utilizzando la seguente proporzione:

2πR : l = 360° : φ

Il primo a calcolare la lunghezza del raggio della Terra fu Eratostene di Cirene in un modo assai elementare.