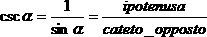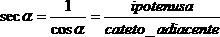Le funzioni trigonometriche
Dato un bastone di lunghezza 1 inclinato di un angolo α rispetto al piano orizzontale, ci chiediamo quanto sia lunga la sua ombra quando il
Sole lo illumina verticalmente. Considerando la figura sottostante,
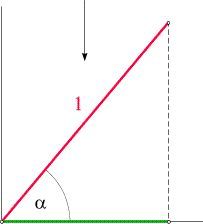
il segmento rosso rappresenta il bastone, la freccia rappresenta la luce che cade dall'alto. L'angolo α è scelto arbitrariamente. Si cerca la lunghezza del segmento verde.
Anche se il problema non è solubile con semplici operazioni di calcolo, tuttavia la lunghezza cercata è univocamente determinata e il suo risultato è chiamato coseno dell’angolo α.
La lunghezza del segmento verde si esprime con cos α. Poiché l'ombra è la lunghezza dell'immagine che il sole "proietta" sulla terra, si può anche dire che cos α è la lunghezza della proiezione di un segmento che è inclinato di un angolo α e ha lunghezza 1. Il simbolo cos α rappresenta quindi un numero reale.
Analogamente si può illuminare il bastone con un raggio di luce in direzione orizzontale e ci si può chiedere quanto sia lunga la sua ombra proiettata su una parete verticale. Anche questa lunghezza in generale non può essere espressa con uno dei metodi di calcolo elementari; essa viene chiamata seno.
La lunghezza del segmento blu nella figura sottostante si esprime con sin α.
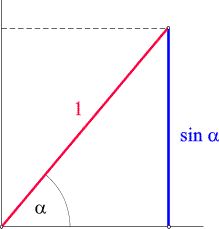
Anche questa volta si tratta di una proiezione, ma ad opera di un raggio di luce orizzontale. Si può anche interpretare sin α come la lunghezza apparente del bastone rosso sullo sfondo visto da una grande distanza.
Seno e coseno e altre grandezze che saranno ricavate in seguito si chiamano funzioni trigonometriche. Il nome "funzione" deriva dal fatto, che a ciascun angolo α si possono assegnare i due numeri sin α e cos α.
Si consideri ora un triangolo rettangolo la cui ipotenusa abbia lunghezza 1 e sia α uno dei due angoli acuti.
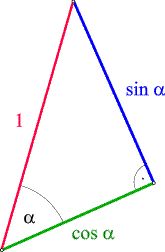
Allora si ha che
• sin α è la lunghezza del cateto opposto all'angolo α, e
• cos α è la lunghezza del cateto adiacente all'angolo α.
Adesso si consideri un triangolo rettangolo con lo stesso angolo α, ma con un' ipotenusa di lunghezza non necessariamente uguale a 1.
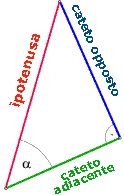
Tale triangolo si ottiene "dilatando" o "riducendo" il triangolo di partenza in maniera tale da mantenere gli angoli. Si dice che il triangolo di partenza e quello ottenuto sono simili. In entrambi i triangoli, il cateto opposto all'angolo α (blu) è più corto rispetto all'ipotenusa di un fattore sin α, e in entrambi i triangoli, il cateto adiacente all'angolo (verde) è più corto rispetto all'ipotenusa di un fattore cos α. In questo senso sin α e cos α possono essere interpretati come fattori di riduzione. Ciò può essere dimostrato formalmente grazie al teorema di Talete.
Si vede quindi che in ogni triangolo rettangolo vale:
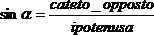
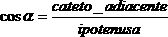
Per illustrare come si utilizzano queste proprietà nei calcoli, consideriamo il seguente problema geodetico: come raffigurato nello schizzo sottostante, la distanza diretta fra un punto di osservazione e la vetta di un monte misura 3.7 km. La vetta appare dal punto di osservazione sotto un angolo di 19.5°. Quanto è alta la montagna?
Soluzione: si consideri il triangolo rettangolo nello schizzo. Usando la relazione relativa al coseno si ottiene:
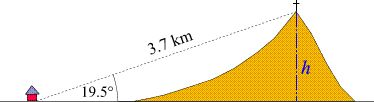
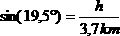
Quindi h = sin(19,5°) × 3.7 km.
Poichè sin(19,5°) = 0.3338, è quindi h = 0.3338 × 3.7 km = 1.24 km, arrotondando il risultato ragionevolmente.
Le definizioni date sopra di seno e coseno in realtà non sono ancora complete. Il seno e il coseno sono stati introdotti come lunghezze dell'ombra di un bastone inclinato di lunghezza 1, rispettivamente sotto un raggio di luce verticale (cos α) e un raggio di luce orizzontale (sin α). Lo raffiguriamo nel disegno sottostante, piazzando un estremo del bastone (rosso) nell'origine di un sistema di coordinate cartesiane e riportando "le ombre" (o meglio proiezioni) lungo gli assi cartesiani. L'angolo α si misura relativamente all'asse orizzontale (delle ascisse) in senso antiorario.
Nella figura sottostante è rappresentato un angolo nel primo quadrante: osserviamo che il seno dell'angolo è positivo e il coseno dello stesso angolo è ancora positivo.
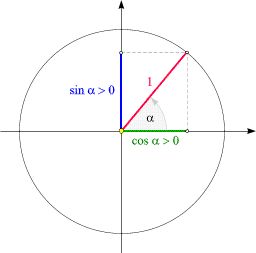
L' angolo α si può aumentare ruotando il bastone rosso come una lancetta di orologio (ma in senso antiorario). La punta della lancetta descrive una circonferenza di raggio 1 detta "circonferenza goniometrica".
Possiamo ruotare il raggio rosso della circonferenza goniometrica e possiamo rappresentare qualsiasi angolo fra 0° e 360°. Nella figura sottostante è rappresentato ora un angolo α nel secondo quadrante. In tal caso, osserviamo che il seno è ancora positivo, ma il coseno è negativo.
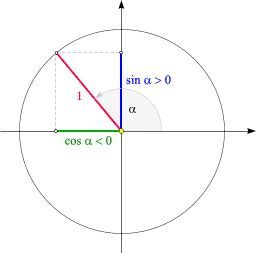
Facendo ancora aumentare l'angolo, possiamo arrivare al terzo quadrante in cui il seno dell'angolo è negativo e così anche il coseno.
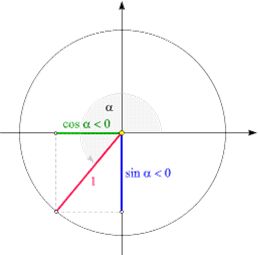
Infine, possiamo considerare un angolo nel quarto quadrante, in cui il seno è negativo, ma il coseno è positivo.
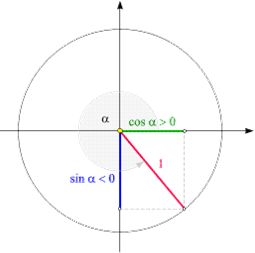
In ogni caso, quindi, riportando le proiezioni del raggio sugli assi cartesiani , possiamo definire il seno e il coseno per un angolo qualsiasi, adottando la seguente convenzione: un segmento orientato verso sinistra oppure verso il basso rispetto all'origine è considerato negativo.
Con l'ausilio della circonferenza goniometrica possiamo dimostrare una serie di proprietà basilari delle funzioni trigonometriche. La circonferenza goniometrica è uno strumento importante per la comprensione di seno e coseno.
Una delle proprietà che si ricavano dalla circonferenza goniometrica riguarda il codominio di seno e coseno: I valori di queste funzioni non possono mai essere minori di 1 o maggiori di 1. Questo si deduce immediatamente dal fatto che le proiezioni del raggio (di lunghezza 1) sugli assi non possono essere più lunghe del raggio stesso.
Le funzioni seno e coseno possiedono varie proprietà. Vediamone alcune.
Consideriamo un triangolo rettangolo, la cui ipotenusa abbia lunghezza 1. Il teorema di Pitagora dice che in un triangolo rettangolo la somma dei quadrati delle lunghezze dei due cateti coincide con il quadrato della lunghezza dell'ipotenusa. Applicandolo al triangolo sottostante,
otteniamo per qualsiasi angolo α l'identità
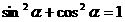
Questa formula fornisce una semplice relazione fra seno e coseno. Se ad esempio, per un certo angolo α, conosciamo sin α, possiamo dedurre
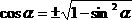
dove il segno dipende dal quadrante in cui si trova il raggio che rappresenta l'angolo α nella circonferenza goniometrica (nel primo e nel quarto quadrante +, altrimenti -).
La circonferenza goniometrica ci mostra che seno e coseno sono funzioni periodiche. Quando a un angolo α sommiamo 360°, il raggio ritorna nella stessa posizione di α. Quindi abbiamo
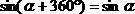
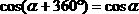
Possiamo dire che il periodo di entrambi le funzioni è 360°. Inoltre abbiamo
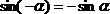
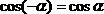
per cui il seno è una funzione antisimmetrica, mentre il coseno è una funzione simmetrica.
Oltre a seno e coseno si usano anche altre funzioni da loro derivate. In particolare i quozienti di seno e coseno hanno un nome proprio: tangente e cotangente. Ecco la definizione:
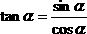
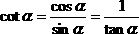
Si noti che queste due espressioni sono reciproche e quindi strettamente legate: il loro prodotto è 1. A volte invece di tan e cot si usano le abbreviazioni tg e ctg.
A differenza del seno e del coseno, per certi angoli la tangente e la cotangente non sono definite. Si provi ad esempio a calcolare tan(90°) oppure cot(0°). Dalle definizioni date sopra infatti deduciamo:
• se cos α = 0 (cosa che si verifica quando α = 90° oppure 270°, dove l'ultimo caso è equivalente a -90), il denominatore nella definizione di tangente diventa zero. In questi casi dunque tan α non è definita, mentre cot α = 0.
• se sin α = 0 (cosa che si verifica quando α = 0° oppure ±180°), il denominatore nella definizione di cotangente diventa zero. In questi casi dunque cot α non è definita, mentre tan α = 0.
Anche la tangente e la cotangente possono essere interpretate come rapporti fra i lati in un triangolo rettangolo.
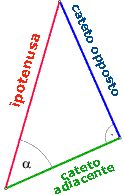
Per le definizioni date prima, si deduce che in un triangolo rettangolo:

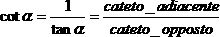
Come esempio applicativo consideriamo il seguente problema geodetico. La vetta di un monte alto 1.24 km viene osservata sotto un angolo di 19.5°. A che distanza si trova l'osservatore dalla proiezione sul piano della vetta del monte?
Soluzione: Consideriamo il triangolo rettangolo nello schizzo.
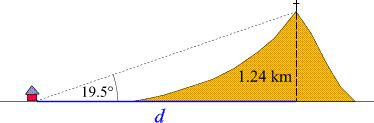
Usiamo la relazione trovata in precedenza:
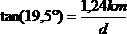
Quindi d = 1.24 km/tan(19.5°). Usando una calcolatrice otteniamo
tan(19.5°) = 0.3541, dunque d = 1.24 km/0.3541 = 3.502 km approssimativamente.
Come per il seno e ilo coseno possiamo utilizzare la circonferenza goniometrica raffigurata qui sotto.
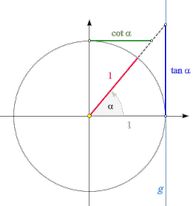
L'angolo α è individuato dal raggio (rosso). La tangente di questo angolo corrisponde alla lunghezza del segmento riportato sulla retta azzurra g. Anche per un angolo ottuso oppure negativo possiamo individuare la tangente sulla stessa retta g. Con questo metodo possiamo anche determinare facilmente il segno per un tale angolo. Nei casi α = 90° e
α = -90° il raggio è parallelo alla retta g. Questa è la spiegazione geometrica del fatto che la tangente non è definita per questi angoli. Per la cotangente valgono proprietà analoghe, scambiando i ruoli degli assi cartesiani.
Consideriamo, ora, altre due funzioni trigonometriche, la cosecante e la secante. Queste ultime, sono rispettivamente l’inverso del seno e del coseno. A differenza di seno e coseno, però, per certi angoli non sono definite. Più precisamente,
• se sin α = 0 (cosa che si verifica quando α = 0° oppure ±180°), il denominatore nella definizione della cosecante diventa zero. In questi casi dunque csc α non è definita.
• se cos α = 0 (cosa che si verifica quando α = 90° oppure 270°, dove l'ultimo caso è equivalente a -90), il denominatore nella definizione della secante diventa zero. In questi casi dunque sec α non è definita.
Anche la cosecante e la secante possono essere interpretate come rapporti fra i lati in un triangolo rettangolo.
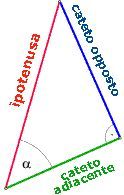
Per le definizioni date prima, si deduce che in un triangolo rettangolo: