La sinusoide è la curva che rappresenta la funzione y =sin(x) nel piano cartesiano.

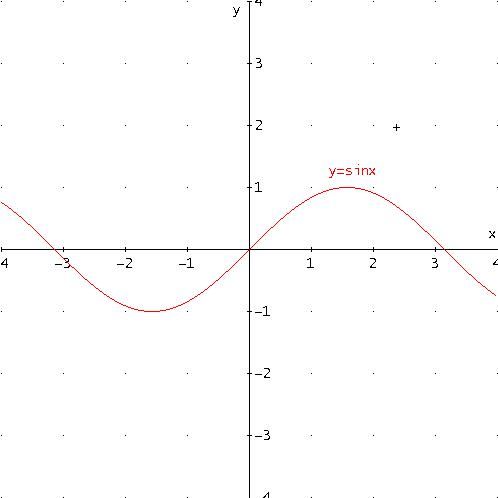
Come si può osservare nel grafico soprastante, che rappresenta una sinusoide, la funzione seno è definita per ogni x appartenente a R. Inoltre è periodica di periodo 2π.

Si chiamano funzioni sinusoidali, invece, quelle funzioni che si possono ottenere dalla funzione y =sin(x) con trasformazioni elementari.

Tracciando i grafici delle funzioni

y =sin(x)

y =sin(-x)

y =-sin(x)

si ottiene la seguente figura:

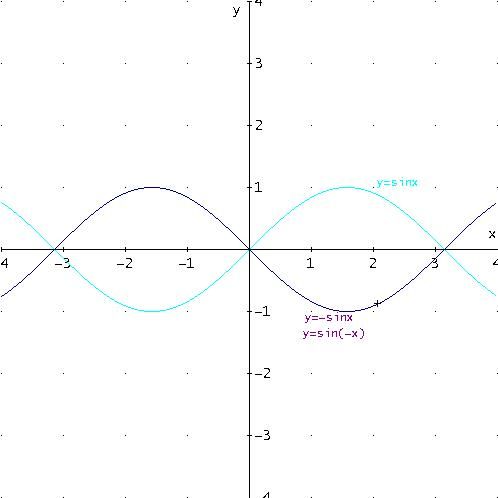
Essa evidenzia che la funzione y =sin(x) è una funzione dispari in quanto

sin(-x) =-sin(x),

per cui essa è simmetrica rispetto all’origine.

Tracciando ancora i grafici delle seguenti funzioni:

y =cos(x)

y =cos(-x)

y =-cosx

si ottiene, invece, la seguente figura:

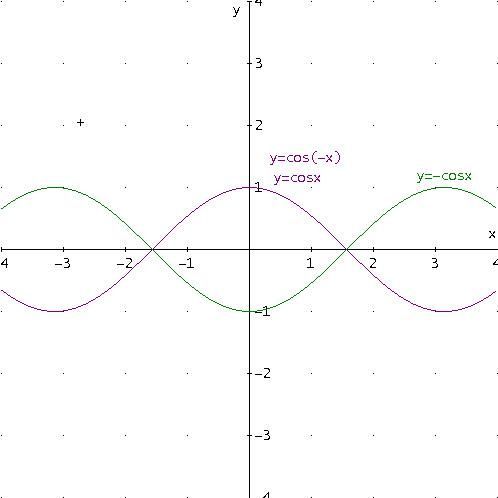
Si deduce, pertanto, che la funzione y =cos(x) è una funzione pari in quanto

cos(-x) =cos(x),

per cui essa è simmetrica rispetto all’asse delle ordinate.

Ora studiamo le curve  y =a∙sin(x) al variare del parametro a.

A tal fine assegniamo ad a i seguenti valori positivi:

a =1

a =1/2

a =2

a =3

a =1/3

Se riportiamo le funzioni corrispondenti su un grafico otteniamo la seguente figura:

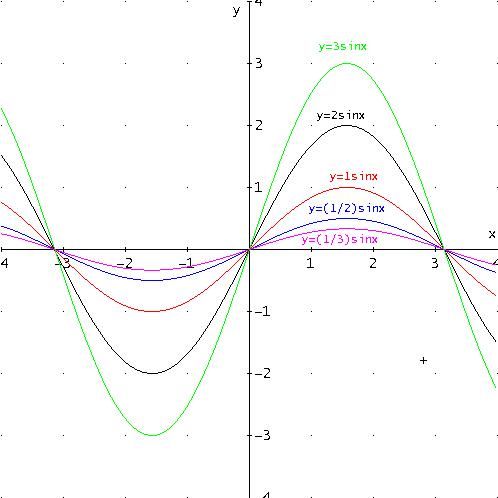
Il confronto con la sinusoide permette di evidenziare una “dilatazione” o una “contrazione” del grafico nella direzione delle ordinate, mantenendo però fissi i punti di ordinata nulla cioè i punti di intersezione con l’asse delle ascisse.

Prendendo sempre in considerazione le curve di equazione y=a∙sinx , proviamo ora ad assegnare ad a i seguenti valori:

a =1

a =-2

a =2

a =-1/2

a =-3

Otteniamo i seguenti grafici:

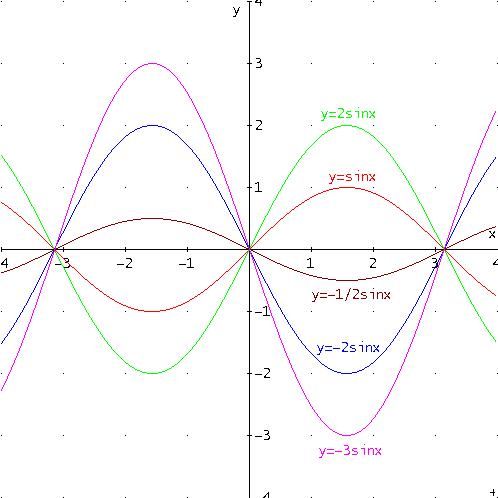
Dalla figura soprastante si può osservare  che, quando a è negativo, i grafici si ottengono dal grafico della funzione y = sin x operando ancora una “dilatazione” o una “contrazione” secondo l’asse delle ordinate, ma anche un ribaltamento rispetto all’asse delle ascisse.

Il valore del parametro a preso in modulo si dice ampiezza della funzione sinusoidale.

Studiamo ora le curve di equazione y =sin(b∙x) assegnando i seguenti valori al parametro b:

b =1

b =2

b =3

b =1/2

b =1/3

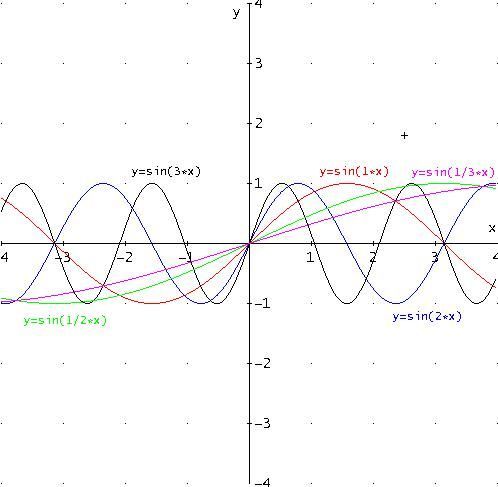
Dal grafico si osserva che il variare di b opera una "contrazione" o una "dilatazione" orizzontali secondo l’asse delle ascisse: più precisamente, al crescere del parametro b si intensifica il numero delle spire. Invece,  l’ampiezza della funzione y =sin(b∙x) è uguale a quella della funzione

y =sin(x).

Tracciamo ora i grafici della funzione y =sin(b∙x) assegnando a b valori negativi:

b =-3

b =-2

b =-1/2

b =-1/3

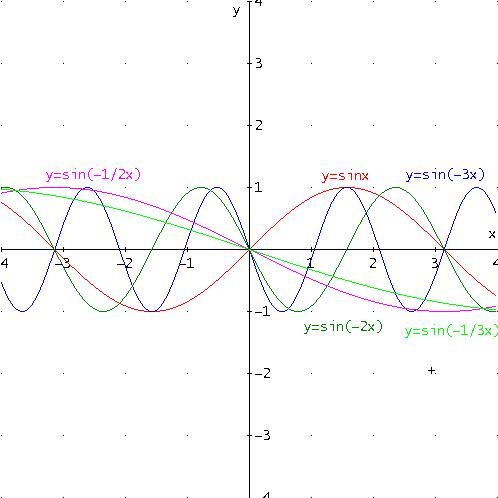
Osservando la figura soprastante si nota che, se b è negativo, c’è ancora una "contrazione" o una "dilatazione" orizzontale secondo l’asse delle ascisse come nel caso precedente, ma anche un ribaltamento.

I grafici delle curve di equazione y = sin(b∙x) consentono di fare alcune osservazioni sul loro periodo.

Il periodo della funzione y = sin x è 2π.

La funzione y = sin(b∙x) compie una oscillazione completa quando la variabile b∙x assume i valori compresi tra 0 e 2π. Da ciò segue immediatamente che il periodo vale 2π/b.

Proviamo ora a studiare le curve di equazione y = sin x + c. Pertanto, tracciamo il grafico delle seguenti funzioni:

y = sin(x)

y = sin(x)+2

y = sin(x)-2

I grafici nella figura soprastante, raffrontati con quello di y = sin x, permettono di concludere che le curve della famiglia y= sinx+c, con c numero reale, sono il risultato di traslazioni verticali della sinusoide, verso l’alto se c>0, verso il basso se c<0.

Analizziamo ora la famiglia di funzioni di equazione y =sin(x-c) con c costante. A tal fine,  quindi, tracciamo il grafico delle seguenti funzioni:

y =sin(x)

y =sin(x-1)

y =sin(x+1)

y =sin(x-2)

y =sin(x+2)

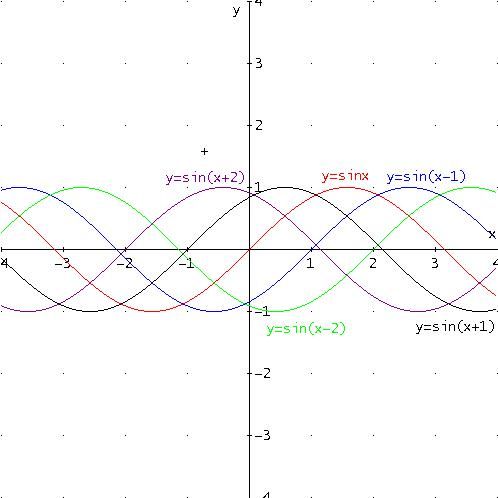
Il confronto con la sinusoide evidenzia una traslazione orizzontale delle curve.

Più precisamente,  si ottiene una traslazione orizzontale lungo l’asse  delle ascisse pari a c unità verso destra se c è positivo, pari a c unità verso sinistra se c è negativo.

Si dice che la funzione y =sin(x-c) è sfasata di una quantità c rispetto alla funzione y =sin(x).

Osserviamo ora i grafici delle funzioni y =sin(x) e y =cos(x):

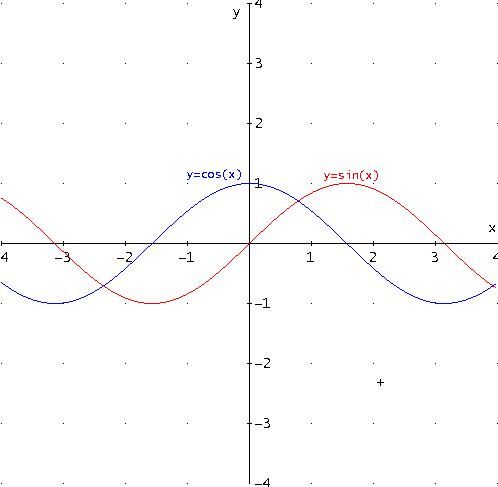
Il grafico della funzione y = cos x non è altro che una traslazione della sinusoide verso sinistra di π/2.

Studiamo ora la famiglia di funzioni di equazione y =a∙sin(x-c). A tal fine tracciamo i grafici delle seguenti funzioni:

y =sin(x)

y =3∙sin(x-1)

y =(1/3) ∙sin(x+1)

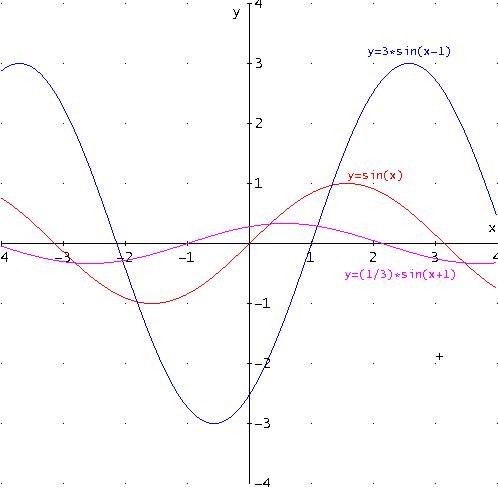
Si ha così una dilatazione o una contrazione secondo l’asse delle ordinate ed una traslazione orizzontale secondo l’asse delle ascisse.

Consideriamo ora il caso in cui una funzione sia data dalla somma algebrica di due o più funzioni. In tal caso il grafico  relativo a tale  funzione  somma algebrica di due o più funzioni si ottiene sommando algebricamente i valori delle ordinate dei punti delle funzioni addendo in corrispondenza dello stesso valore di ascissa. Facciamo alcuni esempi.

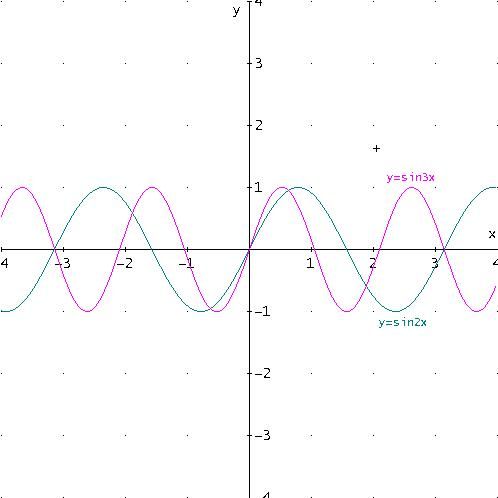
A tal fine, consideriamo le seguenti funzioni di equazione:

y =sin(2x) 

y =sin(3x)

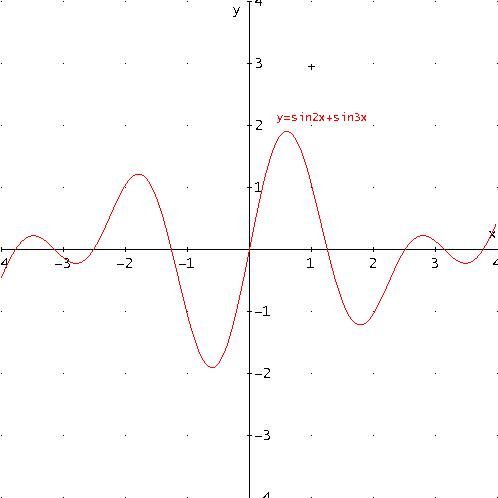
Sommando queste due funzioni si ottiene y =sin2x+sin3x e, pertanto,  il seguente grafico:

Consideriamo ora le funzioni di equazione:

y =sin(x)

y =cos(2x)

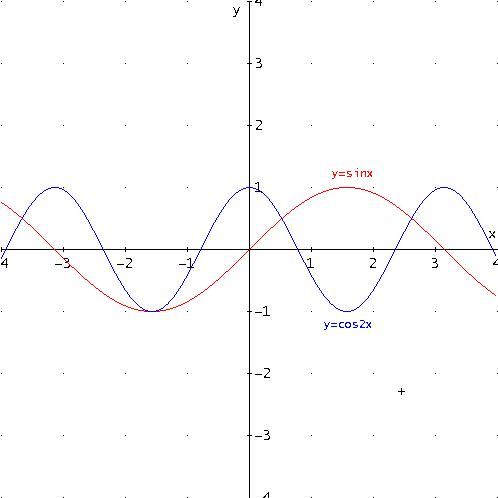
Dopo aver sommato le due funzioni, otteniamo la curva di equazione 

y =sinx+cos2x il cui il grafico è:

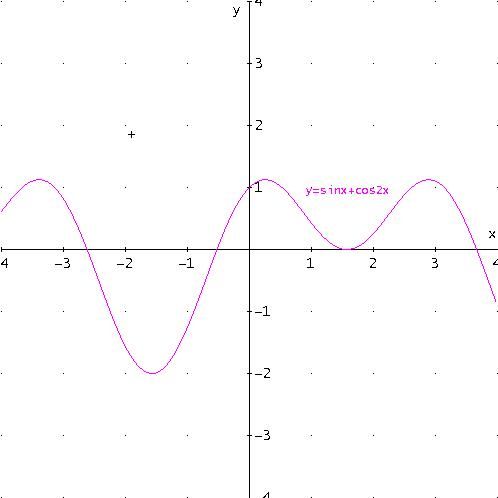
Osserviamo che la funzione risultante non è sinusoidale, ma è periodica di periodo 2π.

Consideriamo ancora le funzioni di equazione:

y =sin(4x)

y =cos(x)

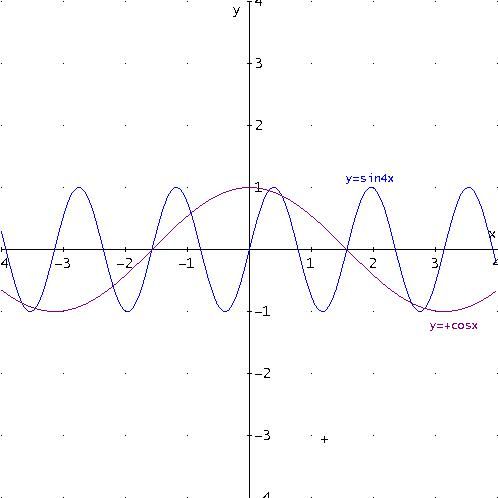
Sottraendole, otteniamo y=sin4x-cosx e, quindi, possiamo tracciare il seguente grafico :

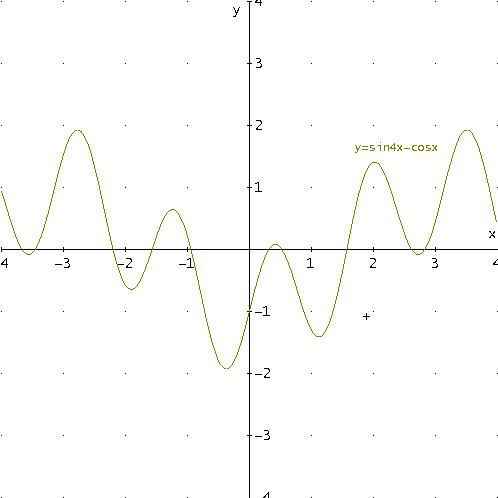
Notiamo che la funzione risultante non è sinusoidale, ma è periodica di

periodo 2π.

Quando si sommano due o più funzioni, dunque, la funzione risultante generalmente non è più una funzione sinusoidale come si può notare nei precedenti esempi. Tuttavia, la funzione risultante è ancora una funzione periodica.

Si potrebbe dimostrare che la sovrapposizione di due funzioni sinusoidali di diverso periodo è una funzione periodica solo se il rapporto fra i due periodi T1 e T2 è un numero razionale. Quindi, deve essere T1/T2=m/n.

Se la frazione m/n è ridotta ai minimi termini, il periodo della funzione risultante è T=nT1=mT2

La somma o sovrapposizione di due funzioni sinusoidali di uguale periodo, invece,  è comunque ancora una funzione sinusoidale di uguale periodo a quello delle funzioni addendo.